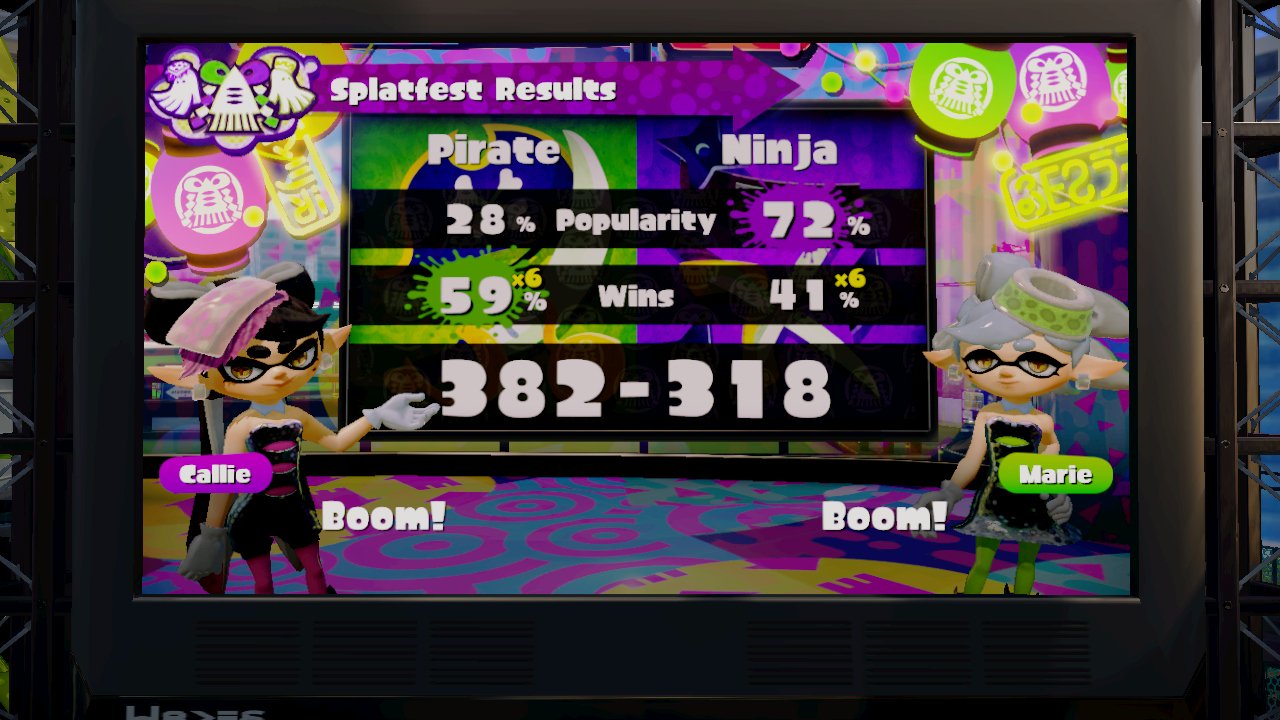
For our hypothetical scenario, we'll start by imagining that a total of 300,000 four-player teams play at some point during Splatfest. (This is just for the sake of an example; don't take this estimate too seriously.)
Let's assume that Ninjas have a precisely 2:1 advantage in popularity--that is, there are exactly twice as many Ninja teams as there are Pirate teams. That's 200,000 Ninja teams and 100,000 Pirate teams.
Now let's make some assumptions about the skill of those teams. Let's assume that:
10% of all teams have an average rank of S
30% of all teams have an average rank of A
40% of all teams have an average rank of B
20% of all teams have an average rank of C
We'll assume that these proportions hold true for each team during the Splatfest. That means that, in total, there are:
10,000 S-rank Pirate teams
30,000 A-rank Pirate teams
40,000 B-rank Pirate teams
20,000 C-rank Pirate teams
and
20,000 S-rank Ninja teams
60,000 A-rank Ninja teams
80,000 B-rank Ninja teams
40,000 C-rank Ninja teams
Now let's take a look at what happens when these teams play against each other. Let's assume that the teams are rather dedicated and end up playing an average of 30 matches each, for a total of 4,500,000 matches. (Remember that it takes 2 teams to play 1 match.) And for the sake of easier calculation, let's assume that a higher-ranked team will always beat a lower-ranked one, and that the teams will win 50% of their matches against teams of equal rank.
Now, since there are twice as many Ninjas as there are Pirates, at any given time, only half of Team Ninja will be playing against Team Pirate. The other half of Team Ninja will be playing against themselves, Ninja vs. Ninja. That means that only half of the matches played by Ninja teams will count toward the final results of the Splatfest. The other half of their matches (1/3 of the total number of matches) can be disregarded, since they are played against their own team.
That means that the breakdown of the actual Pirate vs. Ninja matches will be as follows:
30,000 matches between S-rank Pirates and S-rank Ninjas - 15,000 wins for Pirates, 15,000 wins for Ninjas
90,000 matches between S-rank Pirates and A-rank Ninjas - 90,000 wins for Pirates
120,000 matches between S-rank Pirates and B-rank Ninjas - 120,000 wins for Pirates
60,000 matches between S-rank Pirates and C-rank Ninjas - 60,000 wins for Pirates
90,000 matches between A-rank Pirates and S-rank Ninjas - 90,000 wins for Ninjas
270,000 matches between A-rank Pirates and A-rank Ninjas - 135,000 wins for Pirates, 135,000 wins for Ninjas
360,000 matches between A-rank Pirates and B-rank Ninjas - 360,000 wins for Pirates
180,000 matches between A-rank Pirates and C-rank Ninjas - 180,000 wins for Pirates
120,000 matches between B-rank Pirates and S-rank Ninjas - 120,000 wins for Ninjas
360,000 matches between B-rank Pirates and A-rank Ninjas - 360,000 wins for Ninjas
480,000 matches between B-rank Pirates and B-rank Ninjas - 240,000 wins for Pirates, 240,000 wins for Ninjas
240,000 matches between B-rank Pirates and C-rank Ninjas - 240,000 wins for Pirates
60,000 matches between C-rank Pirates and S-rank Ninjas - 60,000 wins for Ninjas
180,000 matches between C-rank Pirates and A-rank Ninjas - 180,000 wins for Ninjas
240,000 matches between C-rank Pirates and B-rank Ninjas - 240,000 wins for Ninjas
120,000 matches between C-rank Pirates and C-rank Ninjas - 60,000 wins for Pirates, 60,000 wins for Ninjas
The remaining 1,500,000 matches are Ninja vs. Ninja matches, which have no effect on the win rates. In total:
4,500,000 total matches played
1,500,000 wins for Team Pirate
1,500,000 wins for Team Ninja
1,500,000 Ninja vs. Ninja matches (no effect on win rate for either team)