It appears that you are using ad block :'(
Hey, we get it. However this website is run by and for the community... and it needs ads in order to keep running.
Please disable your adblock on Squidboards, or go premium to hide all advertisements and this notice.
Alternatively, this ad may have just failed to load. Woops!
Please disable your adblock on Squidboards, or go premium to hide all advertisements and this notice.
Alternatively, this ad may have just failed to load. Woops!
Next US Splatfest: Pirates VS Ninjas
- Thread starter ShinyGirafarig
- Start date
LimitCrown
Full Squid
- Joined
- Nov 30, 2014
- Messages
- 39
- NNID
- LimitCrown
I wasn't able to participate in this splatfest, unfortunately. I chose Team Ninjas, so that means that I lost.
Also, there really wasn't any point in changing the multiplier; Team Ninjas would have still lost even if the win multiplier was 4, and all that increasing it practically did was make the difference between the scores appear to be larger. There were also a few people that chose Team Pirates mainly because they supposed that the ratio of good players to bad players in Team Ninjas would be lesser because that team would be significantly more popular.
Also, there really wasn't any point in changing the multiplier; Team Ninjas would have still lost even if the win multiplier was 4, and all that increasing it practically did was make the difference between the scores appear to be larger. There were also a few people that chose Team Pirates mainly because they supposed that the ratio of good players to bad players in Team Ninjas would be lesser because that team would be significantly more popular.
Heroine of Squids
Inkling Cadet
- Joined
- Aug 30, 2015
- Messages
- 196
- NNID
- bellpendant
I'm surprised there's so much salt in this thread. Those cheating pirates!
aceofscarabs
Inkling Fleet Admiral
:D
This is just too perfect.
I'm 4-3 on Splatfests now, but I haven't seen this much salt before....ever. I mean, I was pretty pissed on team Autobot and Science, but I don't remember accusing the other side of cheating. We know that people use alternate accounts to sabotage the other team, but that happens too infrequently to matter (or so common that it balances out). How exactly would one team cheat in splatfest? and why does this matter so much?
cwjakesteel
Semi-Pro Squid
I didn't see your analysis. I joined this thread very late.Oh boy. This is going to take a while.
First of all, I'd like to ask you something... Did you actually read my earlier post, in which I crunched all the numbers to show what would actually happen if both teams had equal proportions of skilled and unskilled players? I went to a lot of trouble to do that. If you're going to challenge my conclusion, the least you could do is actually look at my method and point out where it has a relevant flaw.
Second, in your own example, you have chosen a very poor way to illustrate the two teams. If you are going to represent Pirates as a slice of the pie, with the outside (the "crust," if you will) being the good players, then in your full pie that represents Ninjas, you should also let the "crust" of that full pie represent the good players. That would make it far easier to see what happens when you spin the Pirate slice around the pie. (Spoiler alert: It would be perfectly even matchups all around, dooming your theory.) But instead, you chose to represent the skilled Ninja players as another slice of the pie, needlessly complicating matters. And from that mistake springs another flaw...
You have not shown that the slice of good Ninja players is the same proportion of the whole pie as the "crust" of good Pirate players is of the entire slice that represents Pirate players. For all I know just looking at your drawing, you could have underestimated the size of the slice that you needed to properly represent Team Ninja, making it so that Team Pirate actually has a greater proportion of skilled players.
But actually, it's even worse than that, because, without going to the trouble of employing Calculus techniques to precisely calculate everything, I can't even be certain that you didn't overestimate the size of the slice for skilled Ninja players. The problem is that you have grossly oversimplified your analysis, with this summary of "Pirates win" and "Ninjas can win." What actually happens is that, as you spin the full Pirate slice into the slice of skilled Ninja Players, the win rate varies according to how much overlap there is. Depending on the overlap, the win rate for Ninjas could be 40%, 80%, 50.5%, 50.00003%... There are an infinite number of distinct possibilities. You would need to rely on Calculus to accurately assess the results, not this simplistic and vague "Pirates win" and "Ninjas can win."
But, of course, you wouldn't have needed to use Calculus in the first place if you had just chosen a better drawing--one that was easier to analyze correctly... Really, I think that if you had actually read and understood my analysis, you wouldn't have reached such an erroneous conclusion in the first place.
Bottom line: Pirates won more because they had a greater proportion of skilled players, not because of some quirk of the matchmaking process.
Yes the diagram is over-simplified, but it's over-simplified to demonstrate that the principle is true no matter the distribution of players on the different teams.
The proportion of good players to bad players for both teams to be the same is also assumed.
The reason the Pirate's had a crust for good players, and the ninjas a slice, is so that when you spin it like a roulette wheel, they overlap properly, i.e. in the two directions. If for example, I didn't make it a crust, but a slice of the slice (like to the left or right), then all of the slice all the time wouldn't represent the whole Pirate team.
The reason Ninja's don't get a crust, is so that the Pirates and Ninjas can overlap in a cross-section. That's the only way using the pie method to allow for everything to be equal. So having the Ninja be a pie slice doesn't complicate things. I think you're over-complicating the simplicity of it.
You are right when you say,
"What actually happens is that, as you spin the full Pirate slice into the slice of skilled Ninja Players, the win rate varies according to how much overlap there is. Depending on the overlap, the win rate for Ninjas could be 40%, 80%, 50.5%, 50.00003%... There are an infinite number of distinct possibilities."
And that is exactly what the diagram shows. When the game makes a matchup, it's like spinning the wheel, and where it lands determines what match occurs. It's simply showing that it's more likely for the pirate slice to land on the unskilled Ninja sector, than the skilled ninja sector.
You don't need calculus because we're not using exact figures. The diagram is innacurate because it's crudely drawn, but it perfectly portrays what happens, imo.
I.e. there is a chance that the matchup will be completely in favor of pirates, and there's another chance that the patchup will be completely in favour of ninjas. And there's a range for which the chance to win will vary between 100% and 0%. What's confusing about it?
Alright, that bit about the "Ninjas can win vs. Pirates win" was confusing and I should clarify that. What my diagram shows is the chance that the chance to win for any side will be greater than the other.
Also the Pirate Pie and the Ninja pie when added together should equal 100%, Pirates being 28 and Ninjas 72 (as a measure of total area).
Zombie Aladdin
Inkling Fleet Admiral
- Joined
- Aug 19, 2015
- Messages
- 523
- NNID
- Overhazard
Yeah, if there was an uneven proportion of skill between the two teams, that'd be a concern. However, it'd be possible for an unskilled player to drop out and be replaced by a skilled player. When they drop out, chances are likely they'll re-emerge elsewhere.There is also the danger that a skilled Ninja team trying to stick together would suffer from dilution as members drop out and are replaced by lesser players, and given the sheer size of the teampool, the risk of getting unskilled replacements is dramatically higher.
Now, what COULD be a genuine cause is a cushioning effect caused by the ranks. The better the player, the faster he or she will reach the rank he or she wants, and especially upon reaching King or Queen, there's a good chance they'll drop out and end their participation. (That's what I did, but that's because I had to give out candy.) This means the further into a Splatfest there is, the more people there'll be who were good enough to reach King or Queen and stopped playing.
If the distribution of skill was equal, there'd be no gain or loss from this: For every good Team Pirates person who leaves, there will be three good Team Ninjas people who also leave. But it's pretty clear Team Pirates had a higher concentration of highly skilled players. People were likely reaching Pirate King or Queen in proportionally greater numbers faster than Ninja King or Queen. This means the best Team Pirates people will drop out fairly early on while less-skilled people or people who started later take over. This may be the reason behind Team Ninjas gaining a lot of ground in the afternoon and evening: They are now going up against Team Pirates sans a large part of their very best.
This is a pattern I noticed in Art vs. Science too: Art was dominating early on, but Team Science caught up gradually towards the end of the Splatfest. I don't know if it happened with any of the other ones--the only other Splatfest I've played in, Cars vs. Planes, didn't have such a thing: Planes continued to get creamed from beginning to end.
MrL1193
Inkling Cadet
Then please go back and read it. Or, for that matter, check out Zombie Aladdin's dice example here:I didn't see your analysis. I joined this thread very late.
http://squidboards.com/threads/next-us-splatfest-pirates-vs-ninjas.10254/page-7#post-114216
If each team has equal proportions of skilled and unskilled players, then their win rates will be equal as well, regardless of popularity differences. That's all there is to it.
Why would they not overlap properly if you put the skilled Ninjas in a crust instead of a slice? The total population of Ninjas is represented by the entire pie; no matter where you put the Pirates slice, it will fully overlap the Ninja population in some way. I just want you to use the same distribution method for Ninjas as you do for Pirates so that the skill distribution in that overlap will be the same for each team. Just try it and see what happens.The reason the Pirate's had a crust for good players, and the ninjas a slice, is so that when you spin it like a roulette wheel, they overlap properly, i.e. in the two directions. If for example, I didn't make it a crust, but a slice of the slice (like to the left or right), then all of the slice all the time wouldn't represent the whole Pirate team.
The reason Ninja's don't get a crust, is so that the Pirates and Ninjas can overlap in a cross-section. That's the only way using the pie method to allow for everything to be equal. So having the Ninja be a pie slice doesn't complicate things. I think you're over-complicating the simplicity of it.
What you're forgetting is that said matchups will not necessarily favor one team to the same degree. (Again, this problem is caused by your choice to represent skilled Ninjas as a slice instead of just using a "crust" for both Pirates and Ninjas.) If you place your Pirate slice completely on the unskilled Ninja area, the win rate for Pirates might be 55% (because there's only the small "crust" of skilled players giving them an advantage). However, if you instead place the Pirate slice so that it completely overlaps the skilled Ninja slice, Ninjas could enjoy a win rate of as much as 95%. (These numbers are based on an assumption of 10% skilled players.) Thus, even though it's more likely that the slice will end up somewhere that gives Pirates an advantage, the much higher degree to which Ninjas can be favored balances it out.You are right when you say,
"What actually happens is that, as you spin the full Pirate slice into the slice of skilled Ninja Players, the win rate varies according to how much overlap there is. Depending on the overlap, the win rate for Ninjas could be 40%, 80%, 50.5%, 50.00003%... There are an infinite number of distinct possibilities."
And that is exactly what the diagram shows. When the game makes a matchup, it's like spinning the wheel, and where it lands determines what match occurs. It's simply showing that it's more likely for the pirate slice to land on the unskilled Ninja sector, than the skilled ninja sector.
You don't need calculus because we're not using exact figures. The diagram is innacurate because it's crudely drawn, but it perfectly portrays what happens, imo.
I.e. there is a chance that the matchup will be completely in favor of pirates, and there's another chance that the patchup will be completely in favour of ninjas. What's confusing about it?
Proving the end result of all this mathematically would indeed involve Calculus because it's based on a thing called "continuous probability." Feel free to look that up in your own time; I'm not going to attempt to teach it.
That's not actually true as long as the proportions of skilled and unskilled players are the same as they are on the opposing team. Yes, a larger pool of players means that there are more unskilled players that you could get paired up with, but it also means that there are more skilled players that could become your teammates. Thus, it all balances out in the end.There is also the danger that a skilled Ninja team trying to stick together would suffer from dilution as members drop out and are replaced by lesser players, and given the sheer size of the teampool, the risk of getting unskilled replacements is dramatically higher.
(Sorry for the double post; I only just noticed this comment, and I didn't want to bury my reply to it in my longer post.)
Last edited by a moderator:
cwjakesteel
Semi-Pro Squid
EDIT: I put this post in a spoiler because it's worth ignoring. Check my next post.
Yes you would need Calculus to decide the exact probability, but you don't need to do the match when you're two values are "bigger" and "smaller"
Since I didn't see your theory, it wasn't writing it in intended opposition to yours. I was writing it because I thought it was true.
Look, the reason why the Pirates get a crust and the Ninjas get a slice is because it's necessary for the pie diagram. Believe me when I say that if you do it any other way, using the pie-sector method doesn't accurately represent ALL the possible matchups.
That's why one is a slice and the other is a crust, because where ever you spin the wheel, all possible matchups must be represented. If you had it any other way, it would interfere with the results (some matchup types would not be there). When you have it this way, the two extremes of "Great Ninja team vs. Lame Pirate Team" and "Lame Ninja team vs. Great pirate team" and a mix of both are accounted for. That is why one is a pie and the other is a crust. This seems to be your biggest problem with my theory, and I'd like you to see why it's necessary, and an accurate representation. Try it. If you slide the pirate slice over the "good player" ninja slice, you get the whole bag of Perfect vs. terrible, terrible vs. Perfect, mixed vs. mixed. It's the only way the pie diagram can be presented. The pirate slice is divided between good and bad players radially and the ninja pie is divided between good and bad players in sectors. This is how you have to compare overlapping circles (all things equal).
Sorry for all the diagrams, but I drew another one that's more accurate. (I drew the last one 2 am last night).

What you said here:
"What you're forgetting is that said matchups will not necessarily favor one team to the same degree. If you place your Pirate slice completely on the unskilled Ninja area, the win rate for Pirates might be 55% (because there's only the small "crust" of skilled players giving them an advantage). However, if you instead place the Pirate slice so that it completely overlaps the skilled Ninja slice, Ninjas could enjoy a win rate of as much as 95%. (These numbers are based on an assumption of 10% skilled players.) Thus, even though it's more likely that the slice will end up somewhere that gives Pirates an advantage, the much higher degree to which Ninjas can be favored balances it out."
It's very important, and actually, I thought you were right at first, about the degrees. That when the pirates are over the Ninja-win side, they are COMPLETELY COVERED, while when the Pirates are over the Ninja-lose side, they still only win that small crust, so it should be balanced out, and be 50-50 win.
But then I gave it a once-over. You are right when you say the winrate might be 55% if the pirates are over the Ninja-baddies area, while the Ninja's winrate could be as much as 95% if the pirates are over the Ninja-skilled area....and actually, I think you're completely right, and my diagram actually proves that.
Look at the picture when I used the transparency feature. For the over-lap region where the winrate is 50% for both, if we slide the pirate slice upwards, then the winrate would escalate drastically....and the degree to win would be much greater than the degree of when pirates win....
BUT, (and you're right about the degrees), it actually doesn't matter. Again think, about the wheel being spun once for every match. the Ninjas win that match with 95% or 55%, it's still just one win, and the pirates have much more games with >50% to win, than with <50%.
Okay so I read Zombie Alladin's post, and you're right with your diagram (or analogy). But the reason why I think it's not right is because un-skilled players far outnumber skilled players.
My point, if I can say it in a way that makes is that, all of Pirate's skilled players always have a game. Every throw of the green dice, whether you get a 1 or a 6, will match a purple ninja dice from 1-6. But sometimes the Purple 6's get mirror matches.
So you don't even have to roll the green dice, just have all the dice numbers represented, and roll the purple ones. The pirates don't have the chance, per se. because all the pirates are always in play. A number of high purple rolls will be in mirror matches. All high green rolls are in play.
Then please go back and read it. Or, for that matter, check out Zombie Aladdin's dice example here:
http://squidboards.com/threads/next-us-splatfest-pirates-vs-ninjas.10254/page-7#post-114216
If each team has equal proportions of skilled and unskilled players, then their win rates will be equal as well, regardless of popularity differences. That's all there is to it.
Why would they not overlap properly if you put the skilled Ninjas in a crust instead of a slice? The total population of Ninjas is represented by the entire pie; no matter where you put the Pirates slice, it will fully overlap the Ninja population in some way. I just want you to use the same distribution method for Ninjas as you do for Pirates so that the skill distribution in that overlap will be the same for each team. Just try it and see what happens.
What you're forgetting is that said matchups will not necessarily favor one team to the same degree. (Again, this problem is caused by your choice to represent skilled Ninjas as a slice instead of just using a "crust" for both Pirates and Ninjas.) If you place your Pirate slice completely on the unskilled Ninja area, the win rate for Pirates might be 55% (because there's only the small "crust" of skilled players giving them an advantage). However, if you instead place the Pirate slice so that it completely overlaps the skilled Ninja slice, Ninjas could enjoy a win rate of as much as 95%. (These numbers are based on an assumption of 10% skilled players.) Thus, even though it's more likely that the slice will end up somewhere that gives Pirates an advantage, the much higher degree to which Ninjas can be favored balances it out.
Proving the end result of all this mathematically would indeed involve Calculus because it's based on a thing called "continuous probability." Feel free to look that up in your own time; I'm not going to attempt to teach it.
Yes you would need Calculus to decide the exact probability, but you don't need to do the match when you're two values are "bigger" and "smaller"
Since I didn't see your theory, it wasn't writing it in intended opposition to yours. I was writing it because I thought it was true.
Look, the reason why the Pirates get a crust and the Ninjas get a slice is because it's necessary for the pie diagram. Believe me when I say that if you do it any other way, using the pie-sector method doesn't accurately represent ALL the possible matchups.
That's why one is a slice and the other is a crust, because where ever you spin the wheel, all possible matchups must be represented. If you had it any other way, it would interfere with the results (some matchup types would not be there). When you have it this way, the two extremes of "Great Ninja team vs. Lame Pirate Team" and "Lame Ninja team vs. Great pirate team" and a mix of both are accounted for. That is why one is a pie and the other is a crust. This seems to be your biggest problem with my theory, and I'd like you to see why it's necessary, and an accurate representation. Try it. If you slide the pirate slice over the "good player" ninja slice, you get the whole bag of Perfect vs. terrible, terrible vs. Perfect, mixed vs. mixed. It's the only way the pie diagram can be presented. The pirate slice is divided between good and bad players radially and the ninja pie is divided between good and bad players in sectors. This is how you have to compare overlapping circles (all things equal).
Sorry for all the diagrams, but I drew another one that's more accurate. (I drew the last one 2 am last night).

What you said here:
"What you're forgetting is that said matchups will not necessarily favor one team to the same degree. If you place your Pirate slice completely on the unskilled Ninja area, the win rate for Pirates might be 55% (because there's only the small "crust" of skilled players giving them an advantage). However, if you instead place the Pirate slice so that it completely overlaps the skilled Ninja slice, Ninjas could enjoy a win rate of as much as 95%. (These numbers are based on an assumption of 10% skilled players.) Thus, even though it's more likely that the slice will end up somewhere that gives Pirates an advantage, the much higher degree to which Ninjas can be favored balances it out."
It's very important, and actually, I thought you were right at first, about the degrees. That when the pirates are over the Ninja-win side, they are COMPLETELY COVERED, while when the Pirates are over the Ninja-lose side, they still only win that small crust, so it should be balanced out, and be 50-50 win.
But then I gave it a once-over. You are right when you say the winrate might be 55% if the pirates are over the Ninja-baddies area, while the Ninja's winrate could be as much as 95% if the pirates are over the Ninja-skilled area....and actually, I think you're completely right, and my diagram actually proves that.
Look at the picture when I used the transparency feature. For the over-lap region where the winrate is 50% for both, if we slide the pirate slice upwards, then the winrate would escalate drastically....and the degree to win would be much greater than the degree of when pirates win....
BUT, (and you're right about the degrees), it actually doesn't matter. Again think, about the wheel being spun once for every match. the Ninjas win that match with 95% or 55%, it's still just one win, and the pirates have much more games with >50% to win, than with <50%.
Okay so I read Zombie Alladin's post, and you're right with your diagram (or analogy). But the reason why I think it's not right is because un-skilled players far outnumber skilled players.
My point, if I can say it in a way that makes is that, all of Pirate's skilled players always have a game. Every throw of the green dice, whether you get a 1 or a 6, will match a purple ninja dice from 1-6. But sometimes the Purple 6's get mirror matches.
So you don't even have to roll the green dice, just have all the dice numbers represented, and roll the purple ones. The pirates don't have the chance, per se. because all the pirates are always in play. A number of high purple rolls will be in mirror matches. All high green rolls are in play.
Last edited:
Cyrus Dark
Full Squid
Wow, a bunch of dummies on Team Pirate can't do math and keep saying "Oh, it's because our team was full of awesome players, such as myself"
I seriously fought my own team 90% of the matches and I made it to King. The other Team Ninja teams were amazing and completely going to waste.
What a bunch of goobers, if I had been on the winning team and the other side was complaining about endless mirror matches I wouldn't be posting "My Team just had better players."
I assume all the Pirates saying this were also on Team Car and just think they are teh uberness.
I seriously fought my own team 90% of the matches and I made it to King. The other Team Ninja teams were amazing and completely going to waste.
What a bunch of goobers, if I had been on the winning team and the other side was complaining about endless mirror matches I wouldn't be posting "My Team just had better players."
I assume all the Pirates saying this were also on Team Car and just think they are teh uberness.
cwjakesteel
Semi-Pro Squid

Okay, this diagram best represents my thoughts, on why the least popular team wins (I was on team Pirate btw). The dice analogy doesn't work because it's infinite, and in that analogy, you can have everyone as skill 6 at the same time, which doesn't represent reality.
The bright green and purple represent the skilled pirates and ninjas respectively. I also scaled the picture so that the proportions are the same. (The proportion of good to bad players are the same, but actually the proportion of pirates to ninjas doesn't actually represent 28-72 ratio)
If you have any problems with my theory, please refer to this gif. I don't like to make people read walls of text.
Last edited:
Zombie Aladdin
Inkling Fleet Admiral
- Joined
- Aug 19, 2015
- Messages
- 523
- NNID
- Overhazard
No, you're using the crust for Pirates and a slice for Ninjas because your point wouldn't work in any other type of diagram.Look, the reason why the Pirates get a crust and the Ninjas get a slice is because it's necessary for the pie diagram. Believe me when I say that if you do it any other way, using the pie-sector method doesn't accurately represent ALL the possible matchups.
By the way, a mathematical proof is the strongest proof of all. Numbers don't lie. Actuaries don't get six-figure annual incomes for just sitting there movig pie slices around.
Notice that I never once said "skilled players" or "unskilled players" when describing the numbers on the dice. Where an unskilled player ends and a skilled player begins is completely subjective; it's a continuum, not a set of categories. You can set whatever number you like as the minimum to represent good players, but even then, an unskilled team will still likely beat an even less skilled team, and a great team will still likely lose to an even greater team.Okay so I read Zombie Alladin's post, and you're right with your diagram (or analogy). But the reason why I think it's not right is because un-skilled players far outnumber skilled players.
My point, if I can say it in a way that makes is that, all of Pirate's skilled players always have a game. Every throw of the green dice, whether you get a 1 or a 6, will match a purple ninja dice from 1-6. But sometimes the Purple 6's get mirror matches.
So you don't even have to roll the green dice, just have all the dice numbers represented, and roll the purple ones. The pirates don't have the chance, per se. because all the pirates are always in play. A number of high purple rolls will be in mirror matches. All high green rolls are in play.[/spoiler]
You DO have to roll the green die (though they can be any color you want; I used an illustration of 1 green die and 3 purple dice because those were the Splatfest colors) because neither you nor anybody else actually chose which Team Pirates players will be playing. Every Team Pirates member of every skill level will have been playing, and they could find Team Ninjas members of every skill level too. You say all high green rolls are in play, but all low green rolls are in play too.
If you don't believe this randomization system would result in Team Pirates and Team Ninjas having roughly equal win rates, try it yourself. This isn't a trick. It's not a Monty Hall scenario.
This diagram does not accurately analogize to the Splatfest for the reason as the pie chart: You're lumping all of the "skilled" players together like it's some monolithic entity that travel together and play together. In order for that diagram to work, both Team Pirates and Team Ninjas should have even stripes of "skilled" and "unskilled" at equal intervals down the bars.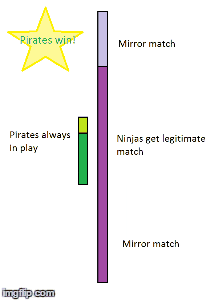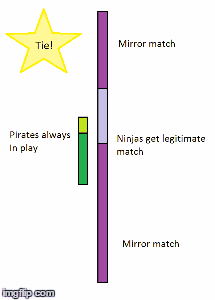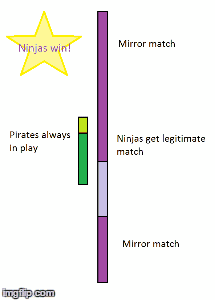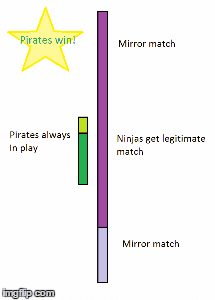
Okay, this diagram best represents my thoughts, on why the least popular team wins (I was on team Pirate btw). The dice analogy doesn't work because it's infinite, and in that analogy, you can have everyone as skill 6 at the same time, which doesn't represent reality.
The bright green and purple represent the skilled pirates and ninjas respectively. I also scaled the picture so that the proportions are the same.
If you have any problems with my theory, please refer to this gif. I don't like to make people read walls of text.
The dice analogy DOES work because there could be as many matches during a Splatfest as Nintendo's servers can handle for that 24-hour period. And you can have top-skilled players facing each other. It's unlikely but possible, just as rolling 6 vs 6 is also an unlikely outcome.
Last edited:
MrL1193
Inkling Cadet
Nope, I was on Team Ninja. Just because you're too salty to admit the truth doesn't mean that I am. The math proves that the popularity difference is not what put Team Ninja at a disadvantage; Pirates won because they had a greater proportion of skilled players. It's as simple as that.Wow, a bunch of dummies on Team Pirate can't do math and keep saying "Oh, it's because our team was full of awesome players, such as myself"
I seriously fought my own team 90% of the matches and I made it to King. The other Team Ninja teams were amazing and completely going to waste.
What a bunch of goobers, if I had been on the winning team and the other side was complaining about endless mirror matches I wouldn't be posting "My Team just had better players."
I assume all the Pirates saying this were also on Team Car and just think they are teh uberness.
You bet I have a problem with your diagram, and it's still the same problem I've been trying to explain to you this whole time. You've oversimplified the results into "Pirates win," "Tie," and "Ninjas win," as if they all have equal weight, but they don't. Whenever your diagram says "Pirates win," Pirates are only winning slightly more matches than they are losing, whereas when your diagram says "Ninjas win," at certain points, Ninjas are winning slightly more than they're losing, but at other times, they're winning an overwhelming majority of their matches. That's why the wins balance out; in your diagram, Pirates can have a smaller advantage for a longer period of time, but Ninjas can have a much bigger advantage for a shorter period of time.If you have any problems with my theory, please refer to this gif. I don't like to make people read walls of text.
And here, I must address a fundamental misunderstanding you seem to have about the meaning of these odds.
The odds do not represent just one match; they represent many thousands of matches. And over the course of those thousands of matches, Pirates are not going to win every one of those matches in which they have a 55-45 advantage; in fact, they're going to lose almost half of them. In contrast, over the course of thousands of matches, Ninjas are going to lose very few of those matches in which they have a 95-5 advantage. Thus, the total wins will indeed balance out over the course of thousands of matches.BUT, (and you're right about the degrees), it actually doesn't matter. Again think, about the wheel being spun once for every match. the Ninjas win that match with 95% or 55%, it's still just one win, and the pirates have much more games with >50% to win, than with <50%.
I think Zombie Aladdin has already addressed the rest of what you said. The only reason you can possibly have for clinging to your "crust and slice" version of your pie diagram is that it gives you a way to argue for your conclusion. That doesn't make it right, though. A "crust and crust" version would absolutely be a valid representation of what's going on, and it would clearly reveal what's really going on.
cwjakesteel
Semi-Pro Squid
Hey, if I'm wrong I'm wrong. Doesn't mean I can't develop the wrong side until it's proven wrong.Nope, I was on Team Ninja. Just because you're too salty to admit the truth doesn't mean that I am. The math proves that the popularity difference is not what put Team Ninja at a disadvantage; Pirates won because they had a greater proportion of skilled players. It's as simple as that.
Zombie Aladdin
Inkling Fleet Admiral
- Joined
- Aug 19, 2015
- Messages
- 523
- NNID
- Overhazard
I should probably mention that, while I picked Team Pirates for this one, I chose Team Planes for the previous Splatfest, and I would absolutely say there was a greater proportion of unskilled players in Team Planes than Team Cars, probably including myself. The level of incompetence I was seeing was staggering, between huddling (where two or more players are right next to each other and facing each other), absolute fear of the opponents, tunnel vision, following teammates and never leaving until one or both of them are splatted, and a refusal to go to where there's enemy ink (particular infurating seeing a roller do this). Sometimes, they're too gung-ho and they run straight into enemy fire with a Splattershot Jr. or an Aerospray MG and get themselves splatted again and again, or I'd put up a Splash Wall for a teammate, only to see them run right up to opponents (not swim through our ink, but run) and get splatted. And sometimes, they don't even bother to ink. They run right up to opponents and get splatted.
I'd guess that what I was seeing being in Team Planes was what was going on with Team Ninjas as well. Whenever we'd win as Team Pirates, Team Ninjas would most often have already been crushed in the first 45 seconds.
In any case, I carry no salt for being on Team Planes, because, when I can afford it and have the time for it, I do prefer traveling through the air than the ground. Thus, I also carry no regrets. We lost.
I'd guess that what I was seeing being in Team Planes was what was going on with Team Ninjas as well. Whenever we'd win as Team Pirates, Team Ninjas would most often have already been crushed in the first 45 seconds.
In any case, I carry no salt for being on Team Planes, because, when I can afford it and have the time for it, I do prefer traveling through the air than the ground. Thus, I also carry no regrets. We lost.
MrL1193
Inkling Cadet
Just to clarify, that remark about saltiness was directed at Geprodis, not you. I know you said you were on Team Pirate.Hey, if I'm wrong I'm wrong. Doesn't mean I can't develop the wrong side until it's proven wrong.
Trieste Sp
Super Moderator
It's alright, just try to avoid it next time.(Sorry for the double post; I only just noticed this comment, and I didn't want to bury my reply to it in my longer post.)
cwjakesteel
Semi-Pro Squid
Okay, but whatever.Just to clarify, that remark about saltiness was directed at Geprodis, not you. I know you said you were on Team Pirate.
I was just sleeping, and then I realized that you guys were right.
But the reason it took me so long to realize, is because you guys kept criticizing my original pie slice/crust diagram, which is COMPLETELY ACCURATE.
I MISINTERPRETED MY OWN DIAGRAM.
The reason the slice/crust diagram is correct is because it's a a coordinate diagram. The Ninja slice represents the x-axis and the pirate slice represents the y-axis.
That's the only way to compare the two interacting teams on a circular plane. Because of that, I made a 3rd diagram (the line gif) and IT WAS COMPLETELY WRONG, because I let the probability shift parallel to each other, rather than perpendicular WHICH WAS PERFECTLY REPRESENTED IN MY PIE DIAGRAM.
So anyway, It's just like you said Mr. L, from the first time, about the degree of wins. When the Ninjas were winning, they were actually winning 95% of the battles, but when the pirates were winning, it was 55%.
So even though the 55% was over a wider area, and the 95% over a smaller area, it amounted to the same amount.
The problem is that I was adding the parts of the pie diagram where the winrate was 50% to the Pirate's aid, when it should have been thrown out.

What I needed to do instead was compare the amount of bright greens that won over the dark purples and the amount of bright purples that won over the dark greens.
AND YOU KNOW WHAT?!?
They're equal.

So there. Also the die analogy that was made is also accurate.
No matter how small the pirate team was, no matter how big or small the proportion of good to bad players are. If they are equal for both teams, then the win chance is also equal. Pirates just won because they had better players (and other random factors that isn't due to matchmaking, unless you consider that it sucks waiting so long to get a match if you're a ninja, which may make you play worse).
LimitCrown
Full Squid
- Joined
- Nov 30, 2014
- Messages
- 39
- NNID
- LimitCrown
Why are we assuming that the proportions of the skill levels of the players in each of the teams are the same? Because of the nature of Splatfests, this is unlikely to be the case because the demographics of each of the two teams would be different from each other. This would explain how an incredibly popular team like Team Ninja would have less skilled players. There's too much focus on the fact that Team Pirates's win percentage was higher instead of the reasons for the win percentage being higher in the first place.
It's unfortunate that popularity is now a nearly insignificant factor in Splatfests because of the increase in the win percentage multiplier from 4 to 6. If one team had a greater popularity percentage and a greater win percentage, then that team would have won anyways. If the difference between the win percentages is greater than or equal to 18% like it was in the previous Splatfest, then it's completely impossible to beat the team with the most wins. Even if the difference in the win percentages weren't that large, it still demonstrates how much of an effect that wins currently have. It also doesn't help that some people chose Team Pirates because they supposed that the opposing team being much more popular would ironically give them an advantage. Splatfests as they are now are very flawed, probably just as much as, if not more than, they were at the beginning.
It's unfortunate that popularity is now a nearly insignificant factor in Splatfests because of the increase in the win percentage multiplier from 4 to 6. If one team had a greater popularity percentage and a greater win percentage, then that team would have won anyways. If the difference between the win percentages is greater than or equal to 18% like it was in the previous Splatfest, then it's completely impossible to beat the team with the most wins. Even if the difference in the win percentages weren't that large, it still demonstrates how much of an effect that wins currently have. It also doesn't help that some people chose Team Pirates because they supposed that the opposing team being much more popular would ironically give them an advantage. Splatfests as they are now are very flawed, probably just as much as, if not more than, they were at the beginning.
Last edited:
Users who are viewing this thread
Total: 5 (members: 0, guests: 5)

